某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取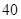 件产品作为样本称出它们的重量(单位:克),重量值落在
件产品作为样本称出它们的重量(单位:克),重量值落在 的产品为合格品,否则为不合格品.图
的产品为合格品,否则为不合格品.图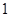 是甲流水线样本的频率分布直方图,表
是甲流水线样本的频率分布直方图,表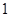 是乙流水线样本频数分布表.
是乙流水线样本频数分布表.
(Ⅰ) 若以频率作为概率,试估计从甲流水线上任取 件产品,求其中合格品的件数
件产品,求其中合格品的件数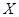 的数学期望;
的数学期望;
(Ⅱ)从乙流水线样本的不合格品中任意取 件,求其中超过合格品重量的件数
件,求其中超过合格品重量的件数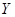 的分布列;
的分布列;
(Ⅲ)由以上统计数据完成下面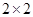 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
| |
甲流水线 |
乙流水线 |
合计 |
| 合格品 |
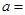 |
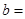 |
|
| 不合格品 |
 |
 |
|
| 合 计 |
|
|
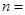 |
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
附:下面的临界值表供参考:
(参考公式: ,其中
,其中 )
)
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线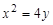 的焦点,且离心率等于
的焦点,且离心率等于 ,直线
,直线 与椭圆C交于M,N两点.
与椭圆C交于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)椭圆C的右焦点F是否可以为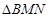 的垂心?若可以,求出直线
的垂心?若可以,求出直线 的方程;若不行,请说明理由.
的方程;若不行,请说明理由.
已知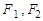 为双曲线
为双曲线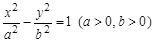 的左、右焦点.
的左、右焦点.
(Ⅰ)若点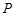 为双曲线与圆
为双曲线与圆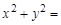
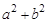 的一个交点,且满足
的一个交点,且满足 ,求此双曲线的离心率;
,求此双曲线的离心率;
(Ⅱ)设双曲线的渐近线方程为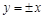 ,
,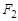 到渐近线的距离是
到渐近线的距离是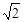 ,过
,过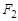 的直线交双曲线于A,B两点,且以AB为直径的圆与
的直线交双曲线于A,B两点,且以AB为直径的圆与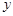 轴相切,求线段AB的长.
轴相切,求线段AB的长.
已知函数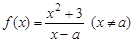 ,其中
,其中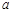 为非零常数.
为非零常数.
(Ⅰ)解关于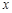 的不等式
的不等式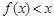 ;
; (Ⅱ)若当
(Ⅱ)若当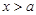 时,函数
时,函数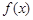 的最小值为3,求实数
的最小值为3,求实数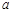 的值.
的值.
已知抛物线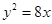 的准线与x轴交于点Q.
的准线与x轴交于点Q.
(Ⅰ)若过点Q的直线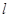 与抛物线有公共点,求直线
与抛物线有公共点,求直线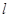 的斜率的取值范围;
的斜率的取值范围;
(Ⅱ)若过点Q的直线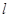 与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
(Ⅰ)已知双曲线C与双曲线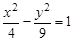 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为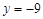 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截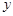 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线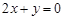 上,并与
上,并与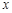 轴相切,求该圆的方程.
轴相切,求该圆的方程.