(本题满分12分)某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为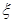 ,求
,求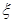 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
(本小题12分)在对人们休闲的一次调查中,共调查了124人,其中女性70人
男性54人.女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性
中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1) 根据以上数据建立一个2×2的列联表;
(2)检验性别是否与休闲方式有关,可靠性有多大?
参考临界值如下
 |
0.05 |
0.025 |
0.01 |
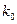 |
3.841 |
5.024 |
6.635 |
(本小题12分)已知函数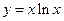
(1)求这个函数的导数;
(2)求这个函数的图像在点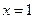 处的切线方程。
处的切线方程。
(本小题满分14分)
用总长14.8m的钢条做一个长方体容器的框架,如果所做容器的底面的一边长比另一边长多0.5m,那么高是多少时容器的容积最大?并求出它的最大容积.
(本小题满分12分)
袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用X表示得分数.
(1)求X的概率分布列;
(2)求X的数学期望EX.
(本小题满分12分)求函数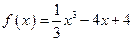 的极值.
的极值.