已知抛物线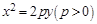 与直线
与直线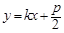 交于A、B两点,O为坐标原点.
交于A、B两点,O为坐标原点.
(I)当k=1时,求线段AB的长;
(II)当k在R内变化时,求线段AB中点C的轨迹方程;
(III)设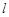 是该抛物线的准线.对于任意实数k,
是该抛物线的准线.对于任意实数k,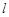 上是否存在点D,使得
上是否存在点D,使得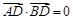 ?如果存在,求出点D的坐标;如不存在,说明理由.
?如果存在,求出点D的坐标;如不存在,说明理由.
已知函数 .
.
(1)写出该函数的单调区间;
(2)若函数 恰有3个不同零点,求实数
恰有3个不同零点,求实数 的取值范围;
的取值范围;
(3)若 对所有
对所有 恒成立,求实数n的取值范围。
恒成立,求实数n的取值范围。
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
标准煤)的几组对照数据:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5="66.5"
用最小二乘法求线性回归方程系数公式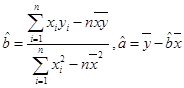 ).
).
已知直线 经过点
经过点 ,且和圆
,且和圆 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 的方程。
的方程。
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”
知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和
频率分布直方图.
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
如图,在棱长为1的正方体 中.
中.
(1)求异面直线 与
与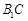 所成的角;
所成的角;
(2)求证平面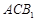 ⊥平面
⊥平面 .
.