下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
标准煤)的几组对照数据:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5="66.5"
用最小二乘法求线性回归方程系数公式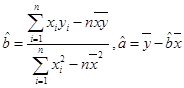 ).
).
已知
,函数
.
(Ⅰ)证明:当
时,
(ⅰ)函数
的最大值为
;
(ⅱ)
;
(Ⅱ) 若
对
[0,1]恒成立,求
的取值范围.
如图,椭圆
的离心率为
,其左焦点到点
的距离为
.不过原点
的直线
与
相交于
两点,且线段
被直线
平分.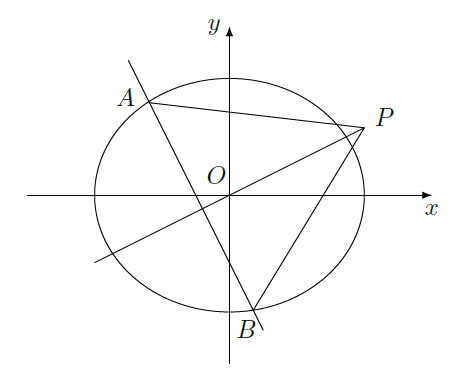
(Ⅰ)求椭圆
的方程;
(Ⅱ) 求
的面积取最大时直线
的方程.
如图,在四棱锥
中,底面是边长为
的菱形,且
,且
平面
,
,
分别为
的中点.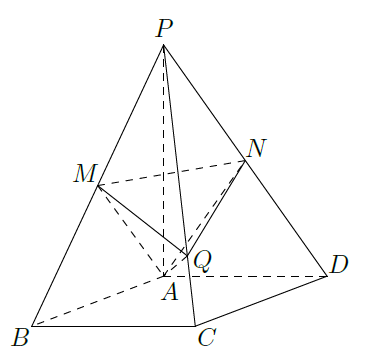
(1)证明:
平面
;
(2) 过点
作
,垂足为点
,求二面角
的平面角的余弦值.
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量
为取出3球所得分数之和.
(Ⅰ)求
的分布列;
(Ⅱ)求
的数学期望
.
已知函数
(1)当
时,求不等式
的解集;
(2)若
的解集包含
,求
的取值范围.