已知二次函数y=x2-2x-3的图象与x轴交于A、B两点
(A在B的左侧),与y轴交于点C,顶点为D。
(1) 求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次
函数的大致图象;
(2) 说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
在平面直角坐标系 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与
),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与 轴,
轴, 轴的另一交点分别为点D,A(如图),连接AM.点P是
轴的另一交点分别为点D,A(如图),连接AM.点P是 上的动点.
上的动点.
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交 轴于点E.
轴于点E.
①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S,求S与t的函数关系式及S的取值范围.
在平面直角坐标系 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于 轴的直线,直线与二次函数
轴的直线,直线与二次函数 的图像相交于点D,E.
的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与 轴相切时,求
轴相切时,求 的值;
的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
我们用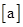 表示不大于
表示不大于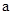 的最大整数,例如:
的最大整数,例如: ,
,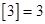 ,
, ;用
;用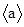 表示大于
表示大于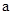 的最小整数,例如:
的最小整数,例如: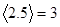 ,
, ,
, .解决下列问题:
.解决下列问题:
(1)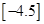 =,,
=,,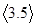 =;
=;
(2)若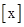 =2,则
=2,则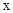 的取值范围是;若
的取值范围是;若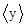 =-1,则
=-1,则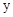 的取值范围是;
的取值范围是;
(3)已知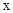 ,
,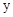 满足方程组
满足方程组 ,求
,求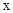 ,
,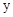 的取值范围.
的取值范围.
某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
| x(元/件) |
38 |
36 |
34 |
32 |
30 |
28 |
26 |
| t(件) |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价-每件服装的进货价)
在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.