如图所示,在平面直角坐标系中,抛物线 (
(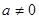 )经过
)经过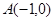 、
、 两点,抛物线与
两点,抛物线与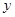 轴交点为
轴交点为 ,其顶点为
,其顶点为 ,连接
,连接 ,点
,点 是线段
是线段 上一个动点(不与
上一个动点(不与 、
、 重合),过点
重合),过点 作
作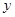 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
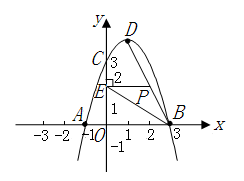
,连接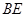 。
。
①求抛物线的解析式,并写出顶点 的坐标;
的坐标;
②如果 点的坐标为(
点的坐标为( ),
),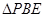 的面积为
的面积为 ,求
,求 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围,并求出
的取值范围,并求出 的最大值;
的最大值;
③在②的条件上,当 取得最大值时,过点
取得最大值时,过点 作
作 的垂线,垂足为
的垂线,垂足为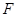 ,连接
,连接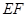 ,把
,把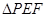 沿直线
沿直线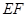 折叠,点
折叠,点 的对应点为
的对应点为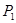 ,请直接写出
,请直接写出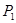 点坐标,并判断点
点坐标,并判断点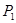 是否在该抛物线上;
是否在该抛物线上;
计算
(1)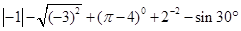
(2)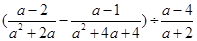 ,其中a满足
,其中a满足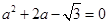
如图1所示,将一个边长为2的正方形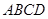 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形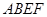 .现将小长方形
.现将小长方形 绕点
绕点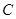 顺时针旋转至
顺时针旋转至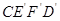 ,旋转角为
,旋转角为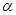 .
.
(1)当点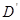 恰好落在
恰好落在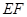 边上时,求旋转角
边上时,求旋转角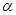 的值;
的值;
(2)如图2,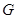 为
为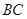 的中点,且0°<
的中点,且0°<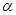 <90°,求证:
<90°,求证: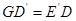 ;
;
(3)先将小长方形 绕点
绕点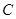 顺时针旋转,使
顺时针旋转,使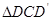 与
与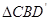 全等(0°<
全等(0°<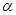 <180°),再将此时的小长方形
<180°),再将此时的小长方形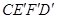 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线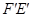 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中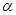 和t的值.
和t的值.
函数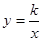 和
和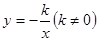 的图象关于y轴对称,我们定义函数
的图象关于y轴对称,我们定义函数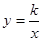 和
和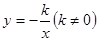 相互为“影像”函数。
相互为“影像”函数。
类似地,如果函数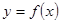 和
和 的图象关于y轴对称,那么我们定义函数
的图象关于y轴对称,那么我们定义函数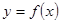 和
和 互为“影像”函数。
互为“影像”函数。
(1)请写出函数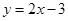 的“影像”函数:;
的“影像”函数:;
(2)函数的“影像”函数是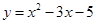 ;
;
(3)如果,一条直线与一对“影像”函数 和
和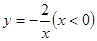 的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数
的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数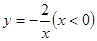 的“影像”函数上的对应点的横坐标是1,求点B的坐标。
的“影像”函数上的对应点的横坐标是1,求点B的坐标。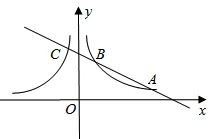
如图①,②,在平面直角坐标系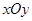 中,点
中,点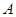 的坐标为(4,0),以点
的坐标为(4,0),以点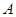 为圆心,4为半径的圆与
为圆心,4为半径的圆与 轴交于
轴交于 ,
,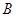 两点,
两点,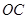 为弦,
为弦,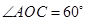 ,
, 是
是 轴上的一动点,连结
轴上的一动点,连结 。
。
(1)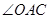 的度数为;
的度数为;
(2)如图①,当 与⊙A相切时,求
与⊙A相切时,求 的长;
的长;
(3)如图②,当点 在直径
在直径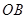 上时,
上时, 的延长线与⊙A相交于点
的延长线与⊙A相交于点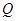 ,问
,问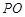 为何值时,
为何值时,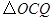 是等腰三角形?
是等腰三角形?
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是m,甲的速度是m/s;
(2)分别写出甲在 和
和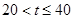 时,y关于t的函数关系式:
时,y关于t的函数关系式:
当 ,y=;当
,y=;当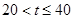 时,y=;
时,y=;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。