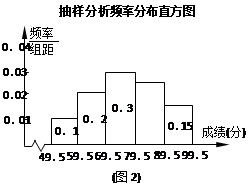
结合“两纲教育”,某中学600名学生参加了“让青春飞扬”知识竞赛.竞赛组委会从中随机抽取了部分学生的成绩(得分都是整数,最高分98分)作为样本进行统计分析,并绘制成抽样分析分类统计表和频率分布直方图(如表1和图2,部分数据缺失).试根据所提供的信息解答下列问题:
(1) 本次随机抽样调查的样本容量是 ;
(2) 试估计全校所有参赛学生中成绩等第为优良的学生人数;
(3) 若本次随机抽样的样本平均数为76.5,又表1中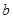 比
比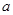 大15,试求出
大15,试求出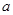 、
、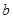 的值;
的值;
(4) 如果把满足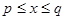 的
的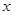 的取值范围记为[
的取值范围记为[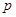 ,
,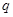 ],表1中
],表1中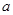 的取值范围是 .
的取值范围是 .
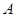 .[69.5,79.5]
.[69.5,79.5] 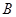 .[65,74]
.[65,74]
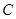 .[66.5,75.5]
.[66.5,75.5] 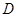 .[66,75]
.[66,75]
|
| 成绩范围 |
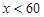 |
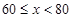 |
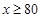 |
| 成绩等第 |
不合格 |
合格 |
优良 |
| 人数 |
|
40 |
|
| 平均成绩 |
57 |
a |
b |
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式.
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价为1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
已知二次函数y= -2x2+8x-6,完成下列各题:
(1)将函数关系式用配方法化为 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
(2)它的图像与x轴交于A,B两点,顶点为C,求S△ABC.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.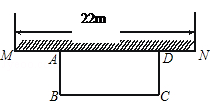
解方程:
(1)
(2)