由四个不同数字1,2,4,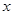 组成无重复数字的三位数,
组成无重复数字的三位数,
⑴若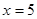 ,其中能被5整除的共有多少个?
,其中能被5整除的共有多少个?
⑵若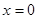 ,其中的偶数共有多少个?
,其中的偶数共有多少个?
⑶若所有这些三位数的各位数字之和是252,求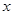 .
.
(本小题满分12分)
国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
序号( ) ) |
每天睡眠时间 (小时) |
组中值( ) ) |
频数 |
频率 (  ) ) |
| 1 |
[4,5) |
4.5 |
8 |
0.04 |
| 2 |
[5,6) |
5.5 |
52 |
0.26 |
| 3 |
[6,7) |
6.5 |
60 |
0.30 |
| 4 |
[7,8) |
7.5 |
56 |
0.28 |
| 5 |
[8,9) |
8.5 |
20 |
0.10 |
| 6 |
[9,10) |
9.5 |
4 |
0.02 |
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少?
(Ⅱ)该网站利用右边的算法流程图,对样本数据作进一步统计分析,求输出的S的值,并说明S的统计意义。
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在 中,
中, ,
, ,
, ,求∠B的值(答案也要修改)
,求∠B的值(答案也要修改)
(本小题满分13分)已知函数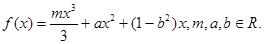
(1)求函数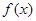 的导函数
的导函数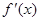 ;
;
(2)当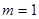 时,若函数
时,若函数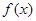 是R上的增函数,求
是R上的增函数,求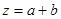 的最小值;
的最小值;
(3)当 时,函数
时,函数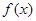 在
在 上存在单调递增区间,求m的取值范围。
上存在单调递增区间,求m的取值范围。
(本小题满分13分)已知矩形 的对角线交于点
的对角线交于点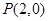 ,边
,边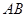 所在直线的方程为
所在直线的方程为 ,点
,点 在边
在边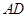 所在的直线上,
所在的直线上,
(1)求矩形 的外接圆的方程;
的外接圆的方程;
(2)已知直线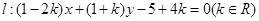 ,求证:直线
,求证:直线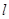 与矩形
与矩形 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线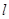 的方程.
的方程.
(本小题满分12分)如图1所示,在 中,
中, ,
, ,
, ,
, 为
为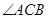 的平分线,点
的平分线,点 在线段
在线段 上,
上,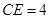 .如图2所示,将
.如图2所示,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,连结
,连结 ,设点
,设点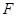 是
是 的中点.
的中点.
(1)求证: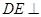 平面
平面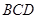 ;
;
(2)若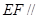 平面
平面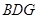 ,其中
,其中 为直线
为直线 与平面
与平面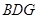 的交点,求三棱锥
的交点,求三棱锥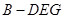 的体积.
的体积.