.已知 是函数
是函数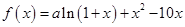 的一个极值点.
的一个极值点.
(1)求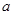 ;
;
(2)求函数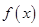 的单调区间.
的单调区间.
(本小题满分14分)
已知函数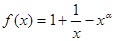 (
( ),且
),且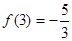 .
.
(1)求α的值;
(2)求函数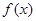 的零点;
的零点;
(3)判断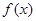 在(-∞,0)上的单调性,并给予证明.
在(-∞,0)上的单调性,并给予证明.
(本小题满分14分)
某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
| 车间 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品自相同车间的概率.
(本小题满分12分)
已知函数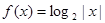 .
.
(1)求函数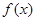 的定义域及
的定义域及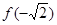 的值;
的值;
(2)判断函数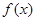 的奇偶性;
的奇偶性;
(3)判断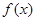 在(0,+∞)上的单调性,并给予证明.
在(0,+∞)上的单调性,并给予证明.
(本小题满分12分)
A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
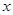 |
80 |
75 |
70 |
65 |
60 |
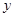 |
70 |
66 |
68 |
64 |
62 |
(1)请根据上表提供的数据,用最小二乘法求出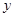 关于
关于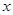 的线性回归方程
的线性回归方程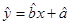 ;
;
(参考数值: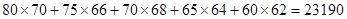 ,
,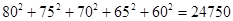 )
)
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(结果保留整数).
(本小题10分)已知数列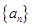 的前
的前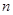 项和
项和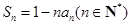 .
.
计算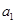 ,
,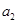 ,
, ,
,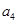 ;
;
猜想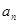 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.