(本小题满分10分)在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程。平面直角坐标系中,直线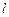
的参数方程是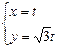 (
(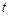 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,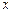 轴的正半轴为极轴,建立极坐
轴的正半轴为极轴,建立极坐
标系,已知曲线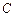 的极坐标方程为
的极坐标方程为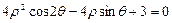 .
.
(I)求直线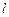 的极坐标方程;
的极坐标方程;
(II)若直线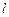 与曲线
与曲线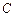 相交于
相交于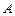 、
、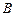 两点,求
两点,求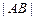 .
.
请考生在(22)、(23)、(24)三题中任选一题作答,如果多答,则按做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑.
(22)(本小题满分10分)选修4—1:几何证明选讲。如图,⊙O是△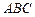 的外接圆,D
的外接圆,D
是的中点,BD交AC于E.
(I)求证:CD =DE·DB;
=DE·DB;
(II)若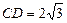 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径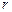 .
.
(本小题满分12分)已知函数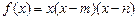 .
.
(I)当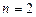 时,若函数
时,若函数 在
在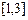 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(II)若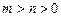 ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求 和
和 的值.
的值.
(本小题满分12分)
已知椭圆
 经过点
经过点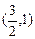 ,一个焦点是
,一个焦点是 .
.
(I)求椭圆 的方程;
的方程;
(II)设椭圆 与
与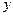 轴的两个交点为
轴的两个交点为 、
、 ,不在
,不在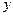 轴上的动点
轴上的动点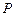 在直线
在直线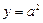 上运动,直线
上运动,直线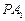 、
、 分别与椭圆
分别与椭圆 交于点
交于点 、
、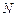 ,证明:直线
,证明:直线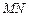 经过焦点
经过焦点 .
.
(本小题满分12分)为预防H1N1病毒爆发,某生物技术公司研制出一种新流感
疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司
选定2000个流感样本分成三组,测试结果如下表:
| 分组 |
A组 |
B组 |
C组 |
| 疫苗有效 |
673 |
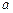 |
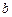 |
| 疫苗无效 |
77 |
90 |
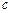 |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(I)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取样本多少个?
(II)已知 ,
, ,求通过测试的概率.
,求通过测试的概率.