(本小题满分12分)
已知椭圆
 经过点
经过点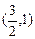 ,一个焦点是
,一个焦点是 .
.
(I)求椭圆 的方程;
的方程;
(II)设椭圆 与
与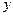 轴的两个交点为
轴的两个交点为 、
、 ,不在
,不在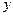 轴上的动点
轴上的动点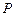 在直线
在直线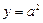 上运动,直线
上运动,直线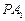 、
、 分别与椭圆
分别与椭圆 交于点
交于点 、
、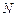 ,证明:直线
,证明:直线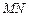 经过焦点
经过焦点 .
.
如图①,E、F分别是直角三角形ABC边AB和AC的中点,∠B=90°,沿EF将三角形ABC折成如图②所示的锐二面角A1EFB,若M为线段A1C中点.求证: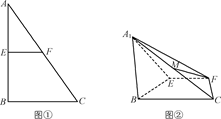
(1)直线FM∥平面A1EB;
(2)平面A1FC⊥平面A1BC.
如图,直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.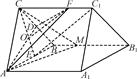
(1)求证:C1E∥平面ADF;
(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF?
如图,三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且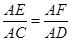 =λ(0<λ<1).
=λ(0<λ<1).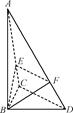
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD..
在直四棱柱ABCDA1B1C1D1中,底面ABCD是菱形.求证:平面B1AC∥平面DC1A1.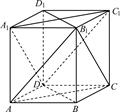
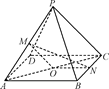
如图,在四棱锥PABCD中,M、N分别是侧棱PA和底面BC边的中点,O是底面平行四边形ABCD的对角线AC的中点.求证:过O、M、N三点的平面与侧面PCD平行.