（年江苏宿迁附加10分）如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．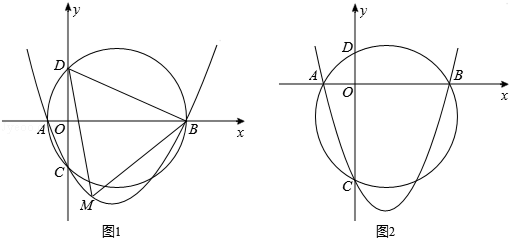
（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的表达式与点D的坐标；
②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；
（2）如图2，若a=1，求证：无论b，c取何值，点D均为定点，求出该定点坐标．
（年江苏南通13分）如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于G．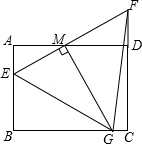
（1）若M为边AD中点，求证：△EFG是等腰三角形；
（2）若点G与点C重合，求线段MG的长；
（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．
（年江苏常州10分）在平面直角坐标系
中，点M（
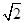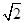,），以点M为圆心，OM长为半径作⊙M ，使⊙M与直线OM的另一交点为点B，与
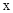轴，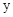
轴的另一交点分别为点D，A（如图），连接AM.点P是
上的动点.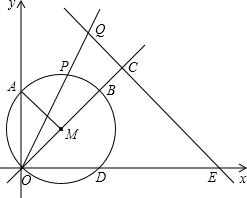
（1）写出∠AMB的度数；
（2）点Q在射线OP上，且OP·OQ=20，过点Q作QC垂直于直线OM，垂足为C，直线QC交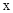轴于点E.
①当动点P与点B重合时，求点E的坐标；
②连接QD，设点Q的纵坐标为t，△QOD的面积为S，求S与t的函数关系式及S的取值范围.
（年吉林长春12分）如图，在矩形ABCD中，AB=4，BC=3，点O为对角线BD的中点，点P从点A出发，沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．
（1）求点N落在BD上时t的值；
（2）直接写出点O在正方形PQMN内部时t的取值范围；
（3）当点P在折线AD﹣DO上运动时，求S与t之间的函数关系式；
（4）直接写出直线DN平分△BCD面积时t的值．
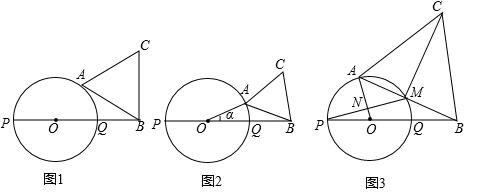
（年湖南株洲8分）如图，PQ为圆O的直径，点B在线段PQ的延长线上，OQ=QB=1，动点A在圆O的上半圆运动（含P、Q两点），以线段AB为边向上作等边三角形ABC．
（1）当线段AB所在的直线与圆O相切时，求△ABC的面积（图1）；
（2）设∠AOB=α，当线段AB、与圆O只有一个公共点（即A点）时，求α的范围（图2，直接写出答案）；
（3）当线段AB与圆O有两个公共点A、M时，如果AO⊥PM于点N，求CM的长度（图3）．
