如图,已知△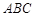 中,∠
中,∠ =90°,
=90°, ,且
,且 =1,
=1, =2,△
=2,△ 绕
绕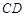 旋转至
旋转至 ,使点
,使点 与点
与点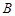 之间的距离
之间的距离 =
= 。
。
(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角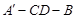 的大小;
的大小;
(3)求异面直线 与
与 所成的角的余弦值。
所成的角的余弦值。
设集合A={x|x2<4},B={x|1<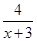 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
已知数列{an}的前n项和Sn=-an- n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式.
(2)设数列 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn>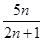 .
.
(3)设数列{cn}满足an(cn-3n)=(-1)n-1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有cn+1>cn.
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),数列{bn}满足b1=1,且点P(bn,bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an},{bn}的通项公式.
(2)求数列{an·bn}的前n项和Dn.
(3)设cn=an·sin2 -bn·cos2
-bn·cos2 (n∈N*),求数列{cn}的前2n项和T2n.
(n∈N*),求数列{cn}的前2n项和T2n.
在平面直角坐标系xOy中,以Ox为始边,角α的终边与单位圆O的交点B在第一象限,已知A(-1,3).
(1)若OA⊥OB,求tan α的值;
(2)若B点横坐标为 ,求S△AOB.
,求S△AOB.
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=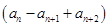 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′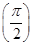 =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2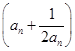 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.