已知圆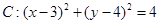
，直线
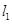过定点A(1，0)．
（Ⅰ）若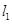与圆相切，求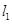的方程；
（Ⅱ）若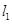与圆相交于P，Q两点，线段PQ的中点为M，又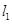与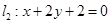
的交点为N，求证:
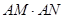为定值．
（本小题满分12分）设函数
其中
（Ⅰ）求
的单调区间；
（Ⅱ） 讨论的极值.
（本小题满分12分） 已知a∈R，求函数f（x）=x2eax的单调区间.
（本小题满分10分）一艘轮船在航行中的燃料费和它的速度的立方成正比，已知在速度为每小时10公里时的燃料费是每小时6元，而其他与速度无关的费用是每小时96元，问此轮船以何种速度航行时，能使行驶每公里的费用总和最小？
（本小题满分12分）某项选拔共有四轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考核，否则即被淘汰．已知某选手能正确回答第一、二、三、四轮的问题的概率分别为
、
、
、
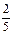，且各轮问题能否正确回答互不影响．
（1）求该选手进入第四轮才被淘汰的概率;
（2）求该选手至多进入第三轮考核的概率． （注：本小题结果可用分数表示）
（本小题满分12分）某单位组织4个部门的职工旅游，规定每个部门只能在韶山、
衡山、张家界3个景区中任选一个，假设各部门选择每个景区是等可能的．
（1）是3个景区都有部门选择的概率是；
（2）求恰有2个景区有部门选择的概率