设函数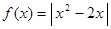 .
.
(1)在区间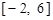 上画出函数
上画出函数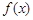 的图象;
的图象;
(2)根据图象写出该函数在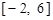 上的单调增区间;
上的单调增区间;
(3)方程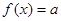 在区间
在区间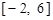 有两个不同的实数根,求
有两个不同的实数根,求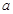 的取值范围.
的取值范围.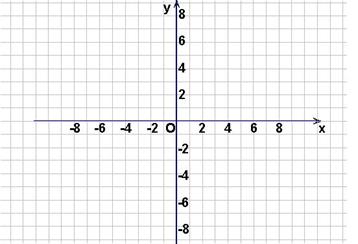
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数: ,
, ,
, ,
, ,
, ,
, .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
盒中装有5个产品,其中3个一等品,2个二等品,从中不放回地取产品,每次1个,求:
(1)取两次,两次都取得一等品的概率;
(2)取两次,第二次取得一等品的概率;
(3)取三次,第三次才取得一等品的概率;
(4)取两次,已知第二次取得一等品,求第一次取得是二等品的概率.
已知数列{ }满足
}满足 =1,
=1, =
= ,(1)计算
,(1)计算 ,
, ,
, 的值;(2)归纳推测
的值;(2)归纳推测 ,并用数学归纳法证明你的推测.
,并用数学归纳法证明你的推测.
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ.
已知函数
(Ⅰ)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求出这条切线的方程;
平行,求出这条切线的方程;
(Ⅱ)若 ,讨论函数
,讨论函数 的单调区间;
的单调区间;
(Ⅲ)对任意的 ,恒有
,恒有 ,求实数
,求实数 的取值范围.
的取值范围.