为了估计某校的某次数学期末考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在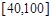 上.将这些成绩分成六段
上.将这些成绩分成六段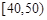 ,
,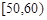 ,…,
,…, 后得到如下部分频率分布直方图.
后得到如下部分频率分布直方图.
(Ⅰ)求抽出的60名学生中分数在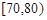 内的人数;
内的人数;
(Ⅱ)若规定成绩不小于85分为优秀,则根据频 率分布直方图,估计该校的优秀人数.
(本小题满分12分)从一批草莓中,随机抽取 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
| 分组(重量) |
 |
 |
 |
 |
| 频数(个) |
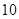 |
 |
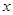 |
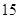 |
已知从 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在 的草莓的概率为
的草莓的概率为 .
.
(1)求出 ,
,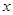 的值;
的值;
(2)用分层抽样的方法从重量在 和
和 的草莓中共抽取
的草莓中共抽取 个,再从这
个,再从这 个草莓中任取
个草莓中任取 个,
个,
求重量在 和
和 中各有
中各有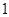 个的概率.
个的概率.
【原创】(本小题满分12分)已知函数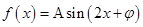 (
(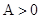 ,
, ),
), 的最大值是
的最大值是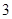 ,其图象经过点
,其图象经过点 .
.
(1)求函数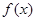 的解析式;
的解析式;
(2)若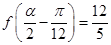 ,求
,求 的值.
的值.
(本小题满分14分)已知函数 在
在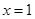 处的切线
处的切线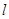 与直线
与直线 垂直,
垂直,
函数 .
.
(1)求实数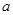 的值;
的值;
(2)若函数 存在单调递减区间,求实数
存在单调递减区间,求实数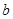 的取值范围;
的取值范围;
(3)设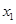 ,
,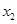 (
(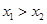 )是函数
)是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值.
的最小值.
(本小题满分14分)已知椭圆
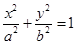 (
(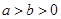 )的右焦点
)的右焦点 ,点
,点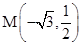
在椭圆 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线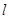 过点
过点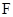 ,且与椭圆
,且与椭圆 交于
交于 ,
,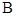 两点,过原点
两点,过原点 作直线
作直线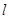 的垂线,垂足为
的垂线,垂足为 ,如果
,如果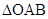 的
的
面积为 (
(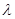 为实数),求
为实数),求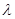 的值.
的值.
【改编】(本小题满分14分)已知数列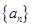 的前
的前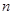 项和是
项和是 ,且
,且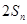 ,
,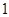 ,
, 成等差数列.
成等差数列.
(1)求数列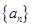 的通项公式;
的通项公式;
(2)设 (
( ),求适合方程
),求适合方程 的正整数
的正整数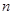 的值.
的值.