根据统计，组装第x件某产品（
），甲工人所用的时间为
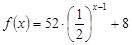，乙工人所用的时间为
（
，
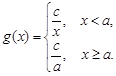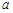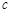为常数）（单位：分钟）．已知乙工人组装第4件产品用时15分钟，组装第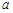件产品用时10分钟．
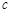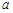（Ⅰ）求和的值；
（Ⅱ）组装第x件某产品，甲工人的用时是否可能多于乙工人的用时？若可能，求出所有x的值；若不可能，请说明理由．
若不等式3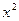
－(6－a)x－b<0的解集是 (－1，3)，求a和b的值．
(满分17分)
已知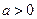
,函数
.
(1)当
时，求所有使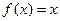
成立的
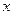的值；
(2)当时，求函数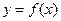
在闭区间
上的最大值和最小值；
(3) 试讨论函数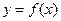的图像与直线
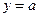的交点个数.
（满分15分）
设函数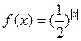
，
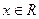
（1）请画出函数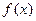
的大致图像；
（2）若不等式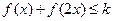
对于任意的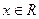恒成立，求实数
的取值范围.
（满分10分）
已知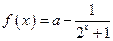
，其中
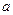为常数
（1）判断
在定义域上的单调性并用单调性的定义证明之；
（2）若函数的定义域为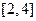
，求函数的最大值和最小值．
（满分10分）
某汽车销售公司以每台10万元的价格销售某种品牌的汽车，可售出该品牌汽车1000台，若将该品牌汽车每台的价格上涨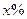
，则销售量将减少
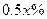，且该品牌汽车每台的价格上涨幅度不超过
，问当该品牌汽车每台的价格上涨百分之几，可使销售的总金额最大？