(本小题满分12分)某公司为了实现2011年1000万元利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润昀25%,现有三个奖励模型: ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由.
(参考数据: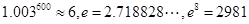 )
)
(本小题满分14分)
设 ,
,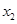 是函数
是函数 的两个极值点,且
的两个极值点,且 ,
,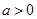 且
且 .
.
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)求证: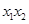 为定值;
为定值;
(3)求 的取值范围.
的取值范围.
(本小题满分12分)如图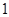 是图
是图 的三视图,三棱锥
的三视图,三棱锥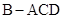 中,
中, ,
,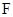 分别是棱
分别是棱 ,
, 的中点.
的中点.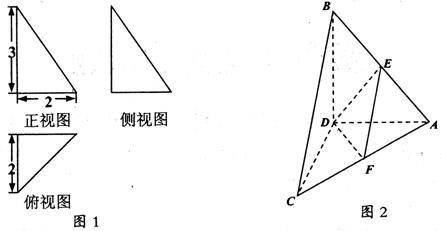
(1)求证: 平面
平面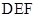 ;
;
(2)求三棱锥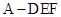 的体积.
的体积.
(本小题满分12分)某学校就一问题进行内部问卷调查.已知该学校有男学生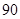 人,女学生
人,女学生 人,教师
人,教师 人,用分层抽样的方法从中抽取
人,用分层抽样的方法从中抽取 人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
(1)请完成此统计表;
(2)根据此次调查,估计全校对这一问题持“同意”意见的人数;
(3)从被调查的女学生中选取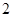 人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
(本小题满分12分)在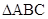 中,角
中,角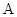 ,
,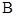 ,
,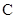 所对的边分别为
所对的边分别为 ,
,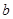 ,
, ,且满足
,且满足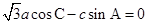 .
.
(1)求角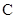 的大小;
的大小;
(2)已知 ,
,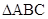 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本小题满分12分)已知等比数列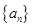 的公比
的公比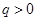 ,
,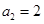 ,
,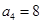 ,等差数列
,等差数列 中
中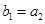 ,
,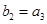 ,其中
,其中 .
.
(1)求数列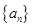 ,
, 的通项公式;
的通项公式;
(2)设数列 ,求数列
,求数列 的前
的前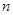 项和
项和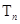 .
.