(13分,文科做)设二次函数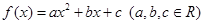 满足下列条件:
满足下列条件:
①当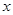 ∈R时,
∈R时,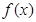 的最小值为0,且f (
的最小值为0,且f (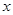 -1)=f(-
-1)=f(-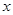 -1)成立;
-1)成立;
②当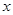 ∈(0,5)时,
∈(0,5)时,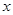 ≤
≤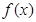 ≤2
≤2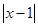 +1恒成立。
+1恒成立。
(1)求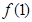 的值;
的值;
(2)求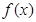 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当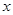 ∈
∈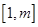 时,就有
时,就有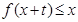 成立。
成立。
为培养高中生综合实践能力和团队合作意识,某市教育部门主办了全市高中生综合实践知识与技能竞赛.该竞赛分为预赛和决赛两个阶段,参加决赛的团队按照抽签方式决定出场顺序.通过预赛,共选拔出甲、乙等六个优秀团队参加决赛.
(Ⅰ)求决赛出场的顺序中,甲不在第一位、乙不在第六位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的团队数记为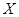 ,求
,求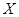 的分布列和数学期望.
的分布列和数学期望.
已知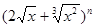 的展开式中,第
的展开式中,第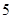 项的二项式系数与第
项的二项式系数与第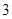 项的二项式系数之比是
项的二项式系数之比是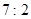 .
.
(Ⅰ)求展开式中含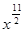 项的系数;
项的系数;
(Ⅱ)求展开式中系数最大的项.
已知函数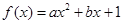 (
(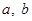 为实数,
为实数,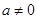 ,
,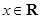 ),
),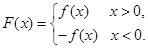
(Ⅰ)若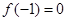 , 且函数
, 且函数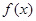 的值域为
的值域为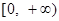 ,求
,求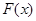 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当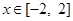 时,
时,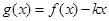 是单调函数,求实数
是单调函数,求实数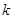 的取值范围;
的取值范围;
(Ⅲ)设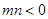 ,
, ,
,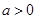 ,且函数
,且函数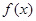 为偶函数,判断
为偶函数,判断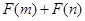 是
是
否大于 ?
?
某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量 与产量
与产量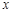 件之间的关系式为:
件之间的关系式为:  ,每件产品的售价
,每件产品的售价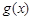 与产量
与产量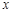 之间的关系式为:
之间的关系式为: 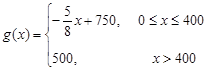 .
.
(Ⅰ)写出该陶瓷厂的日销售利润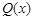 与产量
与产量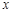 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
已知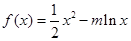 (m
(m R)
R)
(Ⅰ)当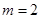 时,求函数
时,求函数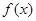 在
在 上的最大,最小值。
上的最大,最小值。
(Ⅱ)若函数 在
在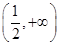 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;