已知函数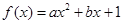 (
(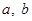 为实数,
为实数,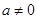 ,
,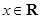 ),
),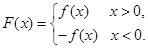
(Ⅰ)若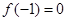 , 且函数
, 且函数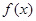 的值域为
的值域为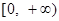 ,求
,求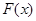 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当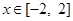 时,
时,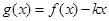 是单调函数,求实数
是单调函数,求实数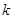 的取值范围;
的取值范围;
(Ⅲ)设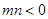 ,
, ,
,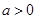 ,且函数
,且函数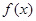 为偶函数,判断
为偶函数,判断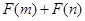 是
是
否大于 ?
?
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
(1)求 ,
, 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
,对 岁的人群随机抽取
岁的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(Ⅰ)补全频率分布直方图并求 、
、 、
、 的值;
的值;
(Ⅱ)从年龄段在 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取 人作为领队,求选取的
人作为领队,求选取的 名领队中恰有1人年龄在
名领队中恰有1人年龄在 岁的概率.
岁的概率.
(本小题满分14分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f(x)= +2a+
+2a+ ,x∈
,x∈ ,其中a是与气象有关的参数,且a∈
,其中a是与气象有关的参数,且a∈ ,若取每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).
,若取每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).
(1)令t= ,x∈
,x∈ ,求t的取值范围;
,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| 感染 |
未感染 |
总计 |
|
| 没服用 |
20 |
30 |
50 |
| 服用 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
(1)求出列联表中数据 的值;
的值;
(2)写出 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:
参考数据:
 |
0.05 |
0.025 |
0.010 |
 |
3.841 |
5.024 |
6.635 |
近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是 .
.
(Ⅰ)求乙、丙各自击中目标的概率.(Ⅱ)求目标被击中的概率.