（本小题满分14分）如图，在四棱锥P—ABCD中，PD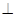
底面ABCD，底面ABCD是正方形，PD=DC，E、F分别为AB、PB的中点。
（1）求证：EF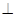 CD；
（2）求DB与平面DEF所成角的正弦值；
（3）在平面PAD内求一点G，使GF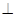 平面PCB，并
证明你的结论。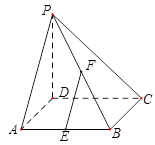
（本小题12分）已知抛物线
，焦点为
，顶点为
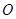，点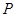
在抛物线上移动，
是
的中点。
（1）求点的轨迹方程；
（2）若倾斜角为60°且过点的直线交的轨迹于
两点，求弦长
。
.（本小题12分）如图，在四棱锥S—ABCD中，
底面ABCD，底面ABCD是平行四边形，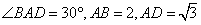
，E是SC的中点。
（1）求证：
；
（2）若SD=2，求二面角E—BD—C的余弦值。
（本小题12分）已知c＞0，设p：函数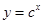
在R上单调递减；q：不等式
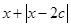＞1的解集为R，如果“p或q”为真，且“p且q”为假，求c的取值范围。
（本小题10分）已知圆与y轴相切，圆心在直线x-3y=0，且这个圆经过点A（6，1），求该圆的方程。
.已知向量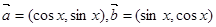
,且
,⑴求
的取值范围;⑵求证
;⑶求函数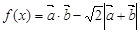
的取值范围.