如图,一个定点滑轮左端通过细绳栓个质量M的物体,右端一个挂一个梯子和质量为 的人处于静止状态,如果要使定滑轮上端的绳子拉力为零,人应如何运动,加速度多大?
的人处于静止状态,如果要使定滑轮上端的绳子拉力为零,人应如何运动,加速度多大?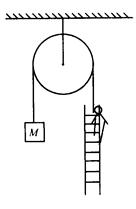
某物体做匀速直线运动,它在20s内通过的路程是160m,它的速度是多少km/h?
某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示。已知该装置密封气体的体积为480cm3,玻璃管内部横截面积为0. 4 cm2,玻璃管在瓶口外的有效长度为48 cm。当气温为7℃时,水银柱刚好处在瓶口位置。
(1)求该气温计能测量的最高气温。
(2)假设水银柱从瓶口处缓慢移动到最右端的过程中,密封气体从外界吸收3J热量,则在这一过程中该气体的内能如何变化?变化了多少?(已知大气压为1 × 105 Pa)
如图(甲)所示,两平行金属板间接有如图(乙)所示的随时间t变化的电压u,两板间电场可看作是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的。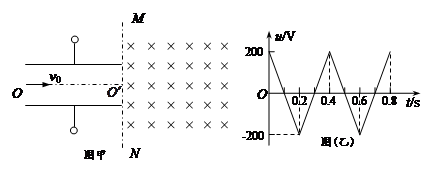
(1)试求带电粒子能够射出电场时的最大电压和对应的射出速度大小。
(2)证明任意时刻从电场射出的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为定值。
(3)从电场射出的带电粒子,进入磁场运动一段时间后又射出磁场。求粒子在磁场中运动的最长时间和最短时间。
如图所示,质量M=3Kg的物块A放在水平桌面上,物块A与桌面的动摩擦因数为μ=0.2,一轻绳跨过光滑的定滑轮连接A和B两个物块,物块B的质量m=1Kg,托起物块B,使物块B距离地面的高度h=0.5m,且轻绳刚好拉直。先由静止释放物块B,已知水平桌面足够长,物块A不会与滑轮相撞,g=10m/s2, 求: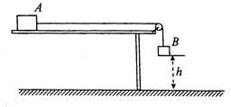
(1)B落地前物块A的加速度大小;
(2)物块A的运动总时间。
如图所示,在光滑水平面上,木块A的质量 ,木块B的质量
,木块B的质量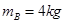 ,质量
,质量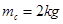 的木块C置于足够长的木块B上,B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止,A以
的木块C置于足够长的木块B上,B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止,A以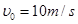 的初速度向右运动,与B碰撞后B的速度为3.5 m/s,碰撞时间极短。求:
的初速度向右运动,与B碰撞后B的速度为3.5 m/s,碰撞时间极短。求:
①A、B碰撞后A的速度。
②弹簧第一次恢复原长时C的速度。