.(本小题满分14分)已知函数 (
( ,
, 是不同时为零的常数),其导函数为
是不同时为零的常数),其导函数为 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少存在一个零点;
内至少存在一个零点;
(3)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线 ,关于
,关于 的方程
的方程 在
在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.
(本小题满 分12分)
分12分)
已知函数 ,
,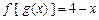 .(1)求
.(1)求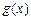 的解析式;(2) 求
的解析式;(2) 求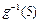 的值.
的值.
已知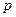 :
: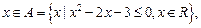
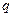 :
: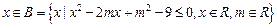 (1)若
(1)若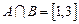 ,求实数
,求实数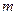 的值;
的值;
(2)若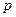 是
是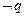 的充分条件,求实数
的充分条件,求实数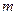 的取值范围.
的取值范围.
(本小题满分14分)
已知函数f(x)的定义域为 ,
, 且同时满足:①f(1)=3;②
且同时满足:①f(1)=3;②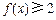 对一切
对一切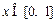 恒成立;③若
恒成立;③若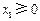 ,
, ,
,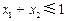 ,则
,则 .
.
①求函数f(x)的最大值 和最小值;
和最小值;
②试比较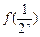 与
与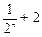
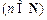 的大小;
的大小;
③某同学发现:当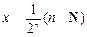 时,有
时,有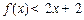 ,由此他提出猜想:对一切
,由此他提出猜想:对一切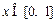 ,都有
,都有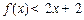 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
(本小题满分14分)
设函数 是定义域在R上的奇函数.
是定义域在R上的奇函数.
(1)若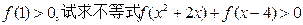 的解集;
的解集;
(2)若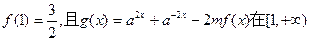 上的最小值为—2,求m的值.
上的最小值为—2,求m的值.
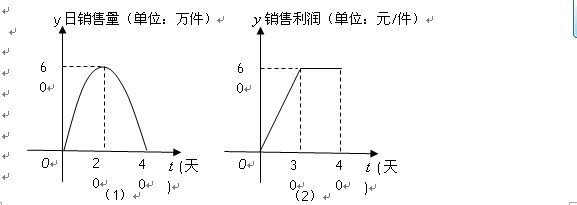
(本小题 满分13分)某公司是专门生产健身产品的企业,第一批产品
满分13分)某公司是专门生产健身产品的企业,第一批产品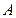 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品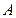 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品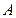 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量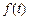 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?