（本小题满分14分）已知函数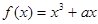
，
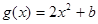，它们的图象在
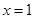处有相同的切线．
（Ⅰ）求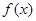
与
的解析式；
（Ⅱ）讨论函数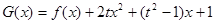
的单调区间；
（Ⅲ）如果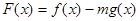
在区间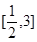
上是单调函数，求实数
的取值范围．
（本小题满分10分）设函数
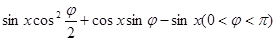在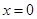
处取最大值．
（1）求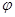
的值;
（2）在
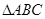中,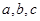
分别是角A,B,C的对边,已知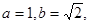
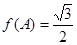,求角C．
（本小题满分10分）已知，（其中）．
（1）求及
；
（2）试比较与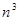
的大小，并说明理由．
已知函数f（x）＝lnx，g（x）＝
ax2＋bx，a≠0.
（Ⅰ）若b＝2，且h（x）＝f（x）－g（x）存在单调递减区间，求a的取值范围；
（Ⅱ）设函数f（x）的图象C1与函数g（x）图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，求证：C1在点M处的切线与C2在点N处的切线不平行.
已知
是函数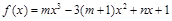
的一个极值点，其中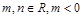
（1）求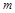
与
的关系式；
（2）求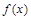
的单调区间；
（3）当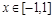
，函数
的图象上任意一点的切线斜率恒大于
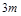，求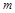的取值范围.
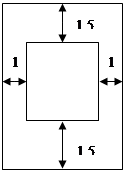
某出版社出版一读物，为了排版设计的需要，规定：一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白，左、右两边各要留1cm宽的空白，出版商为了节约纸张，应选用怎样尺寸的矩形纸张来设计版面？ 