椭圆C1: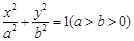 的左、右焦点分别为F1、F2,F2也是抛物线
的左、右焦点分别为F1、F2,F2也是抛物线
C2: 的焦点,点M为C1与C2在第一象
的焦点,点M为C1与C2在第一象 限的交点,且
限的交点,且
(I)求C1的方程;
(II)直线l∥OM(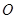 为坐标原点),且与C1交于A、B两点,若
为坐标原点),且与C1交于A、B两点,若 ·
· =0,求直线l的方程
=0,求直线l的方程
(本小题满分13分)
某商场根据调查,估计家电商品从年初(1月)开始的 个月内累计的需求量
个月内累计的需求量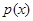 (百件)为
(百件)为
(1)求第 个月的需求量
个月的需求量 的表达式.
的表达式.
(2)若第 个月的销售量满足
个月的销售量满足 (单位:百件),每件利润
(单位:百件),每件利润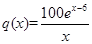 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 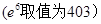
(本小题满分12分)
已知二次函数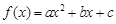 , 满足
, 满足 且
且 的最小值是
的最小值是 .(Ⅰ)求
.(Ⅰ)求 的解析式;(Ⅱ)设函数
的解析式;(Ⅱ)设函数 ,若函数
,若函数 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数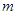 的取值范围。
的取值范围。
(本小题满分12分)
已知函数 (
( ),
),
(Ⅰ)求函数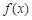 的最小值;
的最小值;
(Ⅱ)已知 ,
, :关于
:关于 的不等式
的不等式 对任意
对任意 恒成立;
恒成立; :函数
:函数 是增函数.若“
是增函数.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知向量 ,
,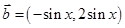 ,函数
,函数
(Ⅰ)求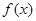 的单调递增区间;
的单调递增区间;
(Ⅱ)在
 中,
中,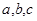 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且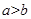 ,求
,求 的值.
的值.
(本小题满分10分)【选修4—5:不等式选讲】
设函数
(I)画出函数 的图象;
的图象;
(II)若关于 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围.