已知数列{bn}的前n项和 .数列{an}满足
.数列{an}满足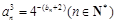 ,数列{cn}满足
,数列{cn}满足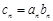 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)若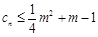 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
画出下列几何体的三视图.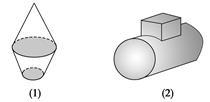
(本小题满分12分)据报道,某公司的33名职工的月工资(以元为单位)如下:
| 职务 |
董事长 |
副董事长 |
董事 |
总经理 |
经理 |
管理员 |
职员 |
| 人数 |
1 |
1 |
2 |
1 |
5 |
3 |
20 |
| 工资 |
5 500 |
5 000 |
3 500 |
3 000 |
2 500 |
2 000 |
1 500 |
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
(本小题满分12分)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
参考公式: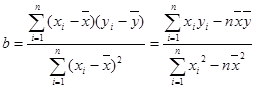
(本小题满分12分)
某种袋装产品的标准质量为每袋100克,但工人在包装过程中一般有误差,规定误差在2克以内的产品均为合格.由于操作熟练,某工人在包装过程中不称重直接包装,现对其包装的产品进行随机抽查,抽查30袋产品获得的数据如下:
| 质量(单位克) |
数量(单位袋) |
 |
2 |
 |
6 |
 |
12 |
 |
8 |
 |
2 |
(1)根据表格中数据绘制产品的频率分布直方图;
(2)估计该工人包装的产品的平均质量的估计值是多少.
(本小题满分12分)对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下
| 甲 |
60 |
80 |
70 |
90 |
70 |
| 乙 |
80 |
60 |
70 |
80 |
75 |
问:甲、乙两人谁的平均成绩高?谁的各门功课发展较平衡?