选修4—5 不等式选讲
设 ,
, ,
,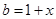 ,
,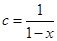 ,试比较
,试比较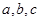 的大小.
的大小.
(要说明理由,最后结果将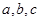 从小到大排列出来)
从小到大排列出来)
已知函数 .
.
(1)讨论函数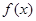 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)已知函数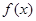 在
在 处取得极值,且对
处取得极值,且对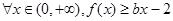 恒成立,求
恒成立,求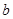 的取值范围.
的取值范围.
已知椭圆 与
与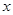 轴、
轴、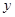 轴的正半轴分别交于
轴的正半轴分别交于 两点,原点
两点,原点 到直线
到直线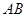 的距离为
的距离为 ,该椭圆的离心率为
,该椭圆的离心率为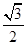 .
.
(1)求椭圆的方程;
(2)是否存在过点 的直线
的直线 与椭圆交于
与椭圆交于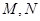 两个不同的点,使
两个不同的点,使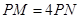 成立?若存在,求出
成立?若存在,求出 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
如图,四棱锥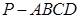 中,底面
中,底面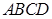 为矩形,
为矩形, 平面
平面 ,
, 是
是 的中点.
的中点.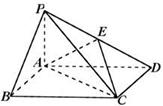
(1)证明: //平面
//平面 ;
;
(2)设 ,三棱锥
,三棱锥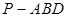 的体积
的体积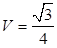 ,求
,求 到平面
到平面 的距离.
的距离.
已知椭圆的两焦点为 ,
,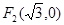 ,离心率
,离心率 .
.
(1)求此椭圆的方程;
(2)设直线 ,若
,若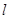 与此椭圆相交于
与此椭圆相交于 ,
,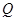 两点,且
两点,且 等于椭圆的短轴长,求
等于椭圆的短轴长,求 的值;
的值;
已知公差不为0的等差数列 的前
的前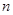 项和为
项和为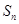 ,
, ,且
,且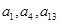 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前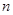 项和公式.
项和公式.