选修4—5:不等式选讲
设正有理数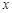 是
是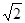 的一个近似值,令
的一个近似值,令 .
.
(Ⅰ)若 ,求证:
,求证: ;
;
(Ⅱ)比较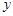 与
与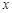 哪一个更接近于
哪一个更接近于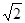 ?
?
已知函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)若函数 在区间
在区间 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知椭圆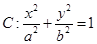
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
(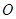 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 取值范围.
取值范围.
已知向量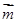
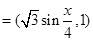 ,
,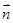
 ,函数
,函数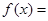

(1)若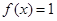 ,求
,求 的值;
的值;
(2)在锐角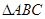 中,角
中,角 的对边分别是
的对边分别是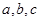 ,且满足
,且满足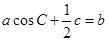 ,
,
求 的取值范围.
的取值范围.
已知三棱锥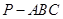 中,
中,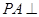 面
面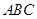 ,
,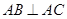 ,
,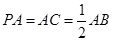 ,
,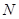 为
为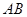 上一点,
上一点,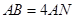 ,
,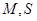 分别为
分别为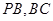 的中点.
的中点.
(1)证明: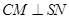 ;
;
(2)求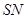 与平面
与平面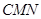 所成角的大小.
所成角的大小.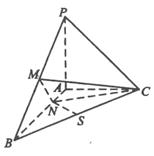
(1)已知等差数列{an}的公差d > 0,且 是方程
是方程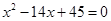 的两根,求数列
的两根,求数列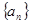 通项公式
通项公式
(2)设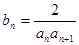 ,求数列{bn}的前n项和
,求数列{bn}的前n项和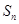 .
.