已知向量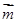
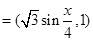 ,
,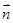
 ,函数
,函数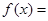

(1)若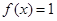 ,求
,求 的值;
的值;
(2)在锐角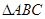 中,角
中,角 的对边分别是
的对边分别是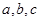 ,且满足
,且满足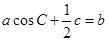 ,
,
求 的取值范围.
的取值范围.
已知定点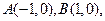 动点
动点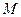 满足
满足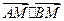 等于点
等于点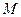 到
到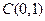 的距离平方的
的距离平方的 倍,试求动点
倍,试求动点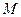 的轨迹方程,并说明方程所表示的曲线。
的轨迹方程,并说明方程所表示的曲线。
如图,已知PA 面ABC,AB
面ABC,AB BC,若PA=AC=2,AB=1
BC,若PA=AC=2,AB=1
(1)求证:面PAB 面PBC; (2)求二面角A-PC-B的正弦值。
面PBC; (2)求二面角A-PC-B的正弦值。
已知数列 的前n项和
的前n项和 满足
满足 ,又
,又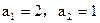
(I)求k的值;(II)求 .
.
已知函数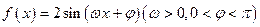 的最小正周期为
的最小正周期为 ,其图像过点
,其图像过点 .
.
(Ⅰ) 求 和
和 的值;(Ⅱ) 函数
的值;(Ⅱ) 函数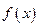 的图像可由
的图像可由 (x∈R)的图像经过怎样的变换而得到?
(x∈R)的图像经过怎样的变换而得到?
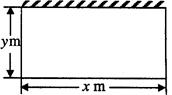
某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为 元
元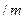 , 两侧的造价为
, 两侧的造价为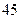 元
元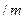 , 顶部的造价为
, 顶部的造价为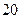 元
元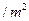 . 设仓库正面的长为
. 设仓库正面的长为 , 两侧的长各为
, 两侧的长各为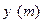 .
. 
(1)用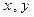 表示这个仓库的总造价
表示这个仓库的总造价 (元);
(元);
(2)若仓库底面面积
 时, 仓库的总造价
时, 仓库的总造价 最少是多少元,
最少是多少元,
此时正面的长应设计为多少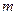 ?
?