在 中,三个内角
中,三个内角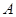 ,
, ,
,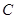 的对边分别为
的对边分别为 ,
, ,
,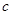 ,其中
,其中 , 且
, 且
(1)求证: 是直角三角形;
是直角三角形;
(2)如图6,设圆 过
过 三点,点
三点,点 位于劣弧上,求
位于劣弧上,求 面积最大值.
面积最大值.
如图5(1)中矩形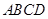 中,已知
中,已知 ,
, ,
, 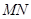 分别为
分别为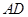 和
和 的中点,对角线
的中点,对角线 与
与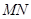 交于
交于 点,沿
点,沿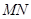 把矩形
把矩形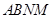 折起,使平面
折起,使平面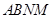 与平面
与平面 所成角为
所成角为 ,如图5(2).
,如图5(2).
(1)求证: ;
;
(2)求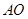 与平面
与平面 所成角的正弦值.
所成角的正弦值.

有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体,从这些小正方体中随机地任取1个,设小正方体涂上颜色的面数为 .
.
(1)求 的概率;
的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
已知等比数列 的前
的前 项和为
项和为 ,
,  ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 通项公式;
通项公式;
(2)设 ,求数列
,求数列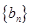 前
前 项和
项和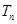 .
.
已知: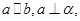 求证:
求证: 。
。