.(本题12分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了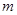 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
,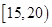 ,
,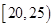 ,
,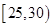 ,
,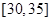 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在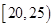 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求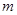 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
设各项均为正数的数列{an}的前n项和为Sn,对于任意的正整数n都有等式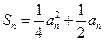
 成立. (1)求数列{an}的通项公式; (2)令数列
成立. (1)求数列{an}的通项公式; (2)令数列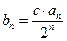 (其中c为正实数),Tn为数列{bn}的前n项和,若Tn>8对n∈N*恒成立,求c的取值范围.
(其中c为正实数),Tn为数列{bn}的前n项和,若Tn>8对n∈N*恒成立,求c的取值范围.
已知定点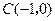 及椭圆
及椭圆 ,过点
,过点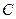 的动直线与椭圆相交于
的动直线与椭圆相交于 两点.
两点.
(Ⅰ)若线段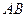 中点的横坐标是
中点的横坐标是 ,求直线
,求直线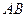 的方程;
的方程;
(Ⅱ)在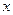 轴上是否存在点
轴上是否存在点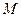 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点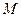 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
甲、乙两个射手进行射击训练,甲击中目标的概率为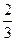 ,乙击中目标的概率为
,乙击中目标的概率为 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
(1)求一个“单位射击组”为“单位进步组”的概率;(2)现要完成三个“单位射击组”,记出现“单位进步组”的次数为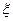 ,求
,求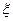 的分布列与数学期望.
的分布列与数学期望.
如图,在正四棱锥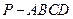 中,
中,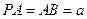 ,点
,点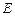 在棱
在棱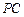 上. (Ⅰ)问点
上. (Ⅰ)问点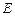 在何处时,
在何处时,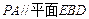 ,并加以证明;(Ⅱ)当
,并加以证明;(Ⅱ)当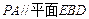 时,求点
时,求点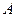 到平面
到平面 的距离;(Ⅲ)求二面角
的距离;(Ⅲ)求二面角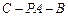 的大小.
的大小.
(本小题满分10分)已知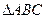 中,
中, ,
,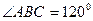 ,
,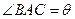 ,
, 记
记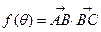 ,
,
(1)求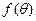 关于
关于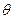 的表达式;
的表达式;
(2)求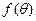 的值域;
的值域;