如右图,在平面直角坐标系 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧 与圆弧
与圆弧 相接而成,两相接点
相接而成,两相接点 均在直线
均在直线 上.圆弧
上.圆弧 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点 ,半径为
,半径为 ;圆弧
;圆弧 过点
过点 .
.
(I)求圆弧 的方程;
的方程;
(II)已知直线 :
: 与“葫芦”曲线
与“葫芦”曲线 交于
交于 两点.当
两点.当 时,求直线
时,求直线 的方程.
的方程.
如图,在直三棱柱 中,
中, 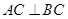 ,
,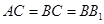 ,点
,点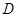 是
是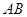 的中点,
的中点,
(1)求证: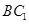 ∥平面
∥平面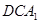 ;
;
(2)设点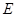 在线段
在线段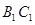 上,
上,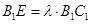 ,且使直线
,且使直线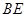 和平面
和平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求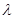 的值.
的值.
在 中,
中, ,
, ,
, ,角
,角 为锐角.
为锐角.
(1)求角 和边
和边 ;(2)求
;(2)求 的值.
的值.
已知 是椭圆
是椭圆 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点
,过椭圆C的右焦点 的直线交椭圆于点
的直线交椭圆于点 ,交直线
,交直线 于点
于点 ,且直线
,且直线 的斜率成等差数列,
的斜率成等差数列, 是椭圆上的两动点,
是椭圆上的两动点, 的横坐标之和为2,
的横坐标之和为2, 的中垂线交
的中垂线交 轴于
轴于 点
点
(1)求椭圆 的方程;(2)求△
的方程;(2)求△ 的面积的最大值
的面积的最大值
如图1,在平面内,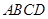 是
是 的矩形,
的矩形,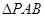 是正三角形,将
是正三角形,将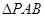 沿
沿 折起,使
折起,使 如图2,
如图2, 为
为 的中点,设直线
的中点,设直线 过点
过点 且垂直于矩形
且垂直于矩形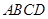 所在平面,点
所在平面,点 是直线
是直线 上的一个动点,且与点
上的一个动点,且与点 位于平面
位于平面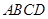 的同侧.
的同侧.
(1)求证: 平面
平面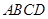 ;
;
(2)设二面角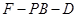 的大小为
的大小为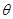 ,若
,若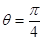 ,求线段
,求线段 的长.
的长.
|

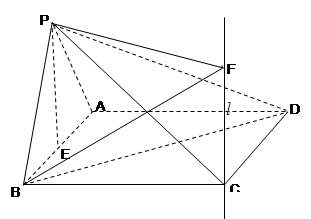
设二次函数 在[-1,4]上的最大值为12,且关于x的不等式
在[-1,4]上的最大值为12,且关于x的不等式 的解集为(0,5).
的解集为(0,5).
(1)求 的解析式;
的解析式;
(2)若对任意的实数x都有 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.