设命题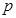 :关于x的函数
:关于x的函数 为增函数;命题
为增函数;命题 :不等式
:不等式 对一切正实数均成立. (1)若命题
对一切正实数均成立. (1)若命题 为真命题,求实数
为真命题,求实数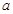 的取值范围;
的取值范围;
(2)命题“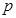 或
或 ”为真命题,且“
”为真命题,且“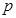 且
且 ”为假命题,求实数
”为假命题,求实数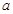 的取值范围.
的取值范围.
如图,已知正三棱柱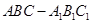 中,
中,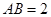 ,
, ,
,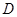 为
为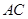 上的动点.
上的动点.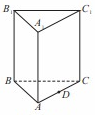
(1)求五面体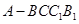 的体积;
的体积;
(2)当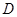 在何处时,
在何处时,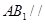 平面
平面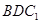 ,请说明理由;
,请说明理由;
(3)当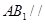 平面
平面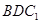 时,求证:平面
时,求证:平面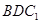
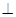 平面
平面 .
.
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下:
得到频率分步表如下:
(1)求表中 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在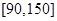 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
已知数列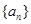 中,
中, ,
,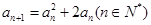 .
.
(1)证明数列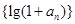 是等比数列,并求数列
是等比数列,并求数列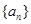 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前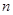 项和
项和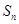 .
.
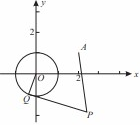
已知点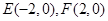 ,曲线
,曲线 上的动点
上的动点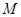 满足
满足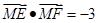 ,定点
,定点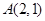 ,由曲线
,由曲线 外一点
外一点 向曲线
向曲线 引切线
引切线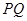 ,切点为
,切点为 ,且满足
,且满足 .
.
(1)求线段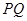 长的最小值;
长的最小值;
(2)若以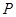 为圆心所作的圆
为圆心所作的圆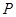 与曲线
与曲线 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆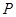 的标准方程.
的标准方程.
定义在 上的函数
上的函数 对任意
对任意 都有
都有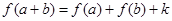 (
( 为常数).
为常数).
(1)判断 为何值时
为何值时 为奇函数,并证明;
为奇函数,并证明;
(2)设 ,
, 是
是 上的增函数,且
上的增函数,且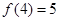 ,若不等式
,若不等式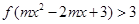 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.