.(本小题满分12分)
某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.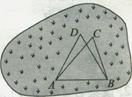
已知抛物线的顶点在原点,它的准线过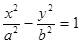 的左焦点,而且与
的左焦点,而且与 轴垂直.又抛物线与此双曲线交于点
轴垂直.又抛物线与此双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程.
分别求满足下列条件的椭圆标准方程.
(1)过点P(1, ),Q(
),Q( ).(2)焦点在x轴上,焦距为4,并且过点
).(2)焦点在x轴上,焦距为4,并且过点
求过点P(1,6),且分别满足下列条件的直线方程:
(1)与直线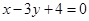 垂直;
垂直;
(2)与圆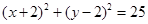 相切
相切
已知函数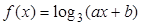 的图象经过点
的图象经过点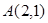 和
和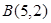 ,记
,记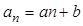 (
(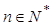 )
)
(1)求数列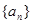 的通项公式;
的通项公式;
(2)设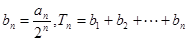 ,若
,若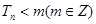 ,求
,求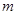 的最小值;
的最小值;
(3)求使不等式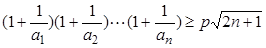 对一切
对一切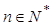 均成立的最大实数
均成立的最大实数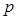 .
.
已知椭圆C: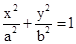 (a>b>0)的离心率为
(a>b>0)的离心率为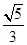 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O:x2+y2=b2的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.