分别求满足下列条件的椭圆标准方程.
(1)过点P(1, ),Q(
),Q( ). (2)焦点在x轴上,焦距为4,并且过点
). (2)焦点在x轴上,焦距为4,并且过点
(本小题满分16分)
已知函数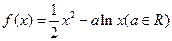
(1)若函数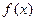 在
在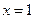 处的切线方程为
处的切线方程为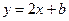 ,求
,求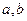 的值;
的值;
(2)任取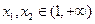 ,且
,且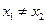 ,恒有
,恒有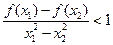 ,求
,求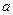 的取值范围;
的取值范围;
(3)讨论方程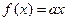 的解的个数,并说明理由。
的解的个数,并说明理由。
(本小题满分16分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(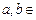 R),
R),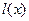 =2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
=2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(1)设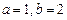 ,若h (x)为偶函数,求
,若h (x)为偶函数,求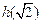 ;
;
(2)设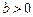 ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
(本小题满分15分)
如图,某市拟在道路AE的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数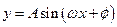 (
(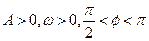 ),
),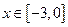 的图象,且图象的最高点为
的图象,且图象的最高点为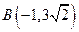 ;赛道的中间部分为
;赛道的中间部分为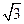 千米的水平跑道
千米的水平跑道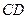 ;赛道的后一部分为以O为圆心的一段圆弧
;赛道的后一部分为以O为圆心的一段圆弧 .
.
(1)求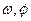 的值和角
的值和角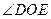 的值;
的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时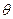 的值.
的值.
(本小题满分15分)
已知函数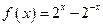 ,
,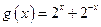 .
.
(1)求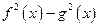 的值;
的值;
(2)证明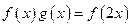 ;
;
(3)若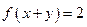 ,
,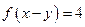 ,求
,求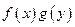 的值.
的值.
(本小题满分14分)
已知命题 :方程
:方程 有两个不相等的负实数根;命题
有两个不相等的负实数根;命题 :函数
:函数 无零点.
无零点.
(1)若 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(2)若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的值的集合.
的值的集合.