已知四棱锥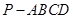 中,
中,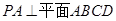 ,底面
,底面 是边长为
是边长为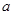 的菱形,
的菱形,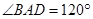 ,
, .
.
(I)求证: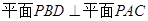 ;
;
(II)设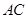 与
与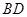 交于点
交于点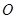 ,
,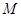 为
为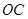 中点,若二面角
中点,若二面角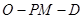 的正切值为
的正切值为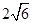 ,求
,求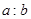 的值.
的值.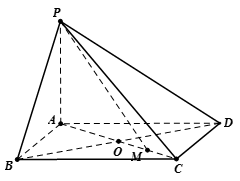
已知函数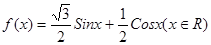
(1)求函数的最小正周期 (2)求函数的单调递增区间 (3)求函数的最大值,并求出对应的X值的取值集合。
已知点A(1,-1),B(5,1),直线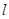 经过点A,且斜率为
经过点A,且斜率为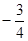 ,
,
(1)求直线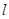 的方程。(2)求以B为圆心,并且与直线
的方程。(2)求以B为圆心,并且与直线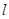 相切的圆的标准方程。
相切的圆的标准方程。
在等比数列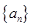 中,
中,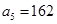 ,公比
,公比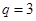 ,前
,前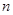 项和
项和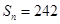 ,求首项
,求首项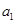 和项数
和项数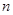 .
.
旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售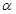 件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为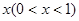 。那么月平均销售量减少的百分率为
。那么月平均销售量减少的百分率为 。改进工艺后,旅游部门销售该纪念品的平均利润是y(元)。
。改进工艺后,旅游部门销售该纪念品的平均利润是y(元)。
(1)写出y与x的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
在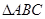 中,角A、B、C所对的边分别为a,b,c,设S为
中,角A、B、C所对的边分别为a,b,c,设S为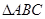 的面积,满足
的面积,满足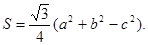
(1)求角C的大小;
(2)求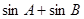 的最大值。
的最大值。