(长为3的线段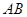 的两个端点
的两个端点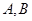 分别在
分别在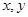 轴上移动,点
轴上移动,点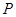 在直线
在直线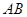 上且满足
上且满足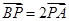 .(I)求点
.(I)求点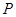 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点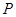 轨迹为曲线
轨迹为曲线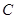 ,过点
,过点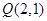 任作直线
任作直线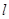 交曲线
交曲线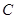 于
于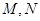 两点,过
两点,过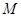 作斜率为
作斜率为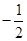 的直线
的直线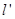 交曲线
交曲线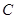 于另一点
于另一点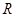 .求证:直线
.求证:直线 与直线
与直线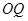 的交点为定点(
的交点为定点(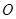 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.
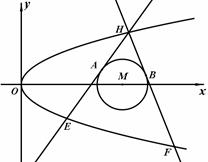
如图,已知抛物线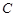 :
: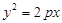 和⊙
和⊙ :
: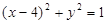 ,过抛物线
,过抛物线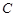 上一点
上一点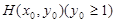 作两条直线与⊙
作两条直线与⊙ 相切于
相切于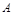 、
、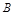 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为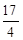 .
.
(1)求抛物线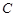 的方程;
的方程;
(2)当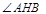 的角平分线垂直
的角平分线垂直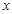 轴时,求直线
轴时,求直线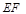 的斜率;
的斜率;
(3)若直线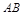 在
在 轴上的截距为
轴上的截距为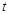 ,求
,求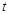 的最小值.
的最小值.
如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED是边长为2的正方形,且所在平面垂直于平面ABC.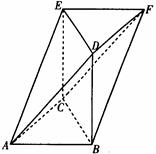
(Ⅰ)求几何体ABCDFE的体积;
(Ⅱ)证明:平面ADE∥平面BCF;
已知数列{an}满足:a1=20,a2=7,an+2﹣an=﹣2(n∈N*).
(Ⅰ)求a3,a4,并求数列{an}通项公式;
(Ⅱ)记数列{an}前2n项和为S2n,当S2n取最大值时,求n的值.
在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足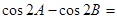

(1)求角 的值;
的值;
(2)若 且
且 ,求
,求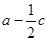 的取值范围.
的取值范围.
已知曲线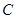 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(Ⅰ)写出直线 的普通方程与曲线
的普通方程与曲线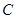 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线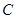 经过伸缩变换
经过伸缩变换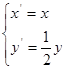 得到曲线
得到曲线 ,设
,设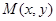 为曲线
为曲线 上任一点,求
上任一点,求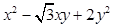 的最小值,并求相应点
的最小值,并求相应点 的坐标.
的坐标.