已知数列{an}满足:a1=20,a2=7,an+2﹣an=﹣2(n∈N*).
(Ⅰ)求a3,a4,并求数列{an}通项公式;
(Ⅱ)记数列{an}前2n项和为S2n,当S2n取最大值时,求n的值.
(本题10分)集合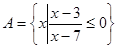 ,
,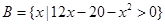 ,求
,求 ,
,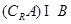 ,
,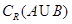 .
.
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求证:f(8)=3
(2)求不等式f(x)-f(x-2)>3的解集.
已知奇函数f(x)=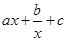 (a、b、c是常数),且满足
(a、b、c是常数),且满足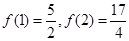
(1)求a、b、c的值
(2)试判断函数f(x)在区间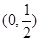 上的单调性并证明
上的单调性并证明
已知函数f(x)是定义在R上的奇函数,当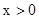 时,
时,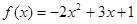 求:
求:
(1)当x<0时,f(x)的解析式
(2)f(x)在R上的解析式