某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.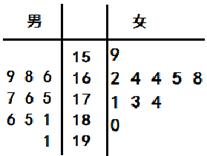
(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.
设函数f(x)= (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=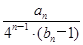 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
正项数列{an}的前n项和Sn满足: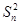 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn=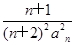 ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< 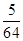 .
.
已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.①当m=48时,求数列{an}的通项公式;②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+…+ak+1-(ak+ak-1+…+a1)=8,k∈N*,求a2k+1+a2k+2+…+a3k的最小值.
知数列{an}是首项为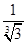 ,公比为
,公比为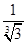 的等比数列,设bn+15log3an=t,常数t∈N*.
的等比数列,设bn+15log3an=t,常数t∈N*.
(1)求证:{bn}为等差数列;
(2)设数列{cn}满足cn=anbn,是否存在正整数k,使ck,ck+1,ck+2按某种次序排列后成等比数列?若存在,求k,t的值;若不存在,请说明理由.