如图,三棱锥 中,
中, 底面
底面 ,
,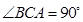 ,
, ,
, 为
为 的中点,点
的中点,点 在
在 上,且
上,且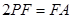 .
.
(1)求证:平面 平面
平面 ;
;
(2)求平面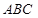 与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.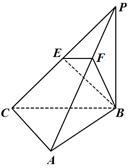
设 ,(1)若
,(1)若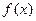 在
在 处有极值,求a;
处有极值,求a;
(2)若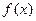 在
在 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
计算由曲线 ,直线x+y=3以及两坐标轴所围成的图形的面积S.
,直线x+y=3以及两坐标轴所围成的图形的面积S.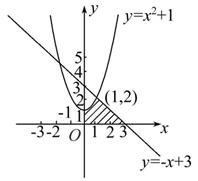
已知函数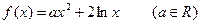 ,设曲线
,设曲线 在点
在点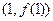 处的切线为
处的切线为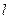 ,若
,若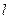 与圆
与圆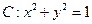 相切,求
相切,求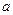 的值.
的值.
(本小题满分12分)
已知函数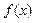 在其定义域上满足
在其定义域上满足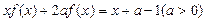 .
.
(1)函数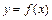 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当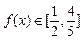 时,求x的取值范围;
时,求x的取值范围;
(3)若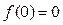 ,数列
,数列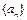 满足
满足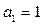 ,那么:
,那么:
①若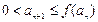 ,正整数N满足
,正整数N满足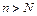 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
,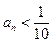 恒成立,求最小的N;
恒成立,求最小的N;
②若 ,求证:
,求证: .
.
(本小题满分12分)
如图,设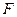 是椭圆
是椭圆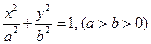 的左焦点,直线
的左焦点,直线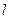 为对应的准线,直线
为对应的准线,直线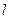 与
与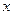 轴交于
轴交于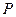 点,
点,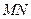 为椭圆的长轴,已知
为椭圆的长轴,已知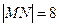 ,且
,且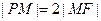 .
.
(1)求椭圆的标准方程;
(2)求证:对于任意的割线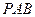 ,恒有
,恒有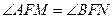 ;
;
(3)求三角形△ABF面积的最大值.