(11分)在一个不透明的纸箱里装有2个红球、1个白球,它们除颜色外完全相同.小明和小亮做摸球游戏,游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你用树状图或列表法说明理由.
如图,ABCD是围墙,AB∥CD,∠ABC=120°,一根6m长的绳子,一端拴在围墙一角的柱子上(B处),另一端拴着一只羊(E处).
(1)请在图中画出羊活动的区域.
(2)求出羊活动区域的面积.
已知 在平面直角坐标系中的位置如下图所示.
在平面直角坐标系中的位置如下图所示.
(1)分别写出图中点
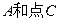 的坐标;
的坐标;(2)画出
 绕点
绕点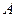 按逆时针方向旋转
按逆时针方向旋转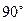 后的
后的 ;
;(3)求点
 旋转到点
旋转到点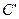 所经过的路线长(结果保留
所经过的路线长(结果保留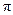 ).
).
(10分).解方程(1)

(2)
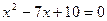
如图,直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60°,AD=3cm,BC=9cm.⊙O1的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts。
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts。
(1)设经过t秒,⊙O2与腰CD相切于点F,过点F画EF⊥DC,交AB于E,则EF=。
(2)过E画EG∥BC,交DC于G,画GH⊥BC,垂足为H.则∠FEG=。
(3)求此时t的值。
(4)在0<t≤3范围内,当t为何值时,⊙O1与⊙O2外切?
如图, 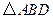 和
和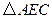 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.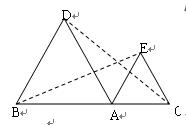
(1)请判断:线段BE与CD的大小关系是;
(2)观察图,当
 和
和 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是,在图4中证明你的猜想.

(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是;它们分别在哪两个全等三角形中;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
