如图,四棱锥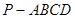 的底面为矩形,
的底面为矩形,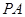 是四棱锥的高,
是四棱锥的高,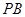 与
与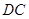 所成角为
所成角为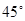 ,
, 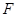 是
是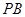 的中点,
的中点,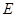 是
是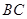 上的动点.
上的动点.
(Ⅰ)证明: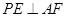 ;
;
(Ⅱ)若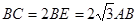 ,求直线
,求直线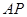 与平面
与平面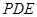 所成角的大小.
所成角的大小.
设定义在R上的奇函数 ,且对任意实数
,且对任意实数 ,恒有
,恒有 ,当
,当 时,
时, 。
。
(1)求证: 是周期函数。(2)当
是周期函数。(2)当 时求
时求 的解析式。
的解析式。
(3)计算 ……+
……+ 。
。
求下列各函数的导数。
(1)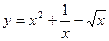 (2)
(2)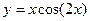
已知函数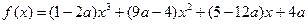 (
( )
)
(1) 当a = 0时, 求函数在区间[0, 2]上的最大值;
(2) 若函数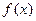 在区间[0, 2]上的最大值为2, 求a的取值范围.
在区间[0, 2]上的最大值为2, 求a的取值范围.
已知数列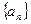 中,
中,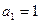 ,
,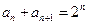 (n∈N*),
(n∈N*),
(1)试证数列 是等比数列,并求数列{
是等比数列,并求数列{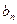 }的通项公式;
}的通项公式;
(2)在数列{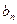 }中,求出所有连续三项成等差数列的项;
}中,求出所有连续三项成等差数列的项;
(3)在数列{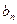 }中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
}中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
已知函数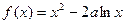 (
( ).
).
(1)讨论函数 的单调性;
的单调性;
(2)若关于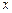 的方程
的方程 有唯一解,求
有唯一解,求 的值.
的值.