城市的空气质量以其空气质量指数API（为整数）衡量，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显．根据空气质量指数API的不同，可将空气质量分级如下表：
| API |
0~50 |
51~100 |
101~150 |
151~200 |
201~250 |
251~300 |
>300 |
| 状况 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重污染 |
重度污染 |
为了了解某城市2011年的空气质量情况，现从该城市一年空气质量指数API的监测数据库中，用简单随机抽样方法抽取30个空气质量指数API进行分析，得到如下数据：
| API分组 |
 |
 |
 |
 |
 |
 |
 |
| 频数 |
2 |
1 |
4 |
6 |
10 |
5 |
2 |
（Ⅰ）完成下面频率分布直方图，并求质量指数API的中位数大小；
（Ⅱ）估计该城市一年中空气质量为优良的概率；
（Ⅲ）请你依据所给数据和上述分级标准，对该城市的空气质量给出一个简短评价.
（本小题满分12分）已知f (x)＝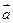
·
－1，其中向量＝（
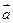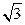sin2x，cosx），＝（1，2cosx）（x∈R）
（Ⅰ）求f (x)的单调递减区间；
（Ⅱ）在△ABC中，角A、B、C的对边分别为a、b、c，f (A)＝2，a＝
，b＝，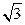
求边长c的值。
（本小题满分16分）过原点O作圆x2+y2-8x=0的弦OA。
求弦OA中点M的轨迹方程；
（2）如点
是（1）中的轨迹上的动点，
①求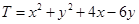
的最大、最小值；
②求
的最大、最小值。
（本小题满分14分）求圆心在直线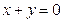
上，且过两圆
，
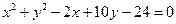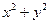
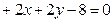交点的圆的方程。
（本小题满分14分）已知圆与y轴相切，圆心在直线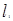
: x-3y=0上，且在直线
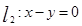上截得的弦长为
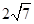，求该圆的方程.
（本小题满分14分）已知圆C：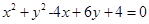
（1）将圆C的方程化成标准方程并指出圆心C的坐标及半径的大小；
（2）过点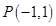
引圆C的切线，切点为A，求切线长
；
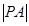（3）求过点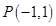的圆C的切线方程；