(本小题共13分)已知圆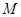 过两点
过两点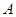 (1,-1),
(1,-1), (-1,1),且圆心
(-1,1),且圆心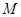 在
在 上.
上.
(1)求圆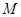 的方程;
的方程;
(2)设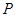 是直线
是直线 上的动点,
上的动点,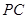 、
、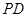 是圆
是圆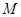 的两条切线,
的两条切线,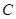 、
、 为切点,求四边形
为切点,求四边形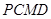 面积的最小值.
面积的最小值.
(本小题满分12分)已知顶点在坐标原点,焦点在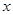 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点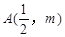 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设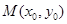 为抛物线上的一个定点,过
为抛物线上的一个定点,过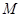 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦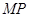 ,
,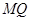 ,求证:
,求证: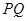 恒过定点
恒过定点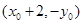 .(3)直线
.(3)直线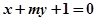 与抛物线交于
与抛物线交于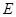 ,
,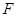 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点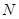 ,使得△
,使得△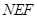 为以
为以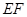 为斜边的直角三角形.
为斜边的直角三角形.
(本小题满分12分)已知椭圆
 的离心率为
的离心率为 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,
, ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点 且斜率不为
且斜率不为 的直线交椭圆
的直线交椭圆 于
于 ,
, 两点.试问
两点.试问 轴上是否存在定点
轴上是否存在定点 ,使
,使 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分12分)如图,已知三棱柱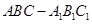 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, ,
, ,
, 分别是
分别是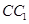 ,
, 的中点,点
的中点,点 在直线
在直线 上,且
上,且 ;
;
(1)证明:无论 取何值,总有
取何值,总有 ;
;
(2)当 取何值时,直线
取何值时,直线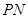 与平面
与平面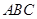 所成的角
所成的角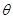 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(3)是否存在点 ,使得平面
,使得平面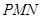 与平面
与平面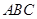 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(本小题满分12分)在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ;
(本小题满分10分)如图,在直三棱柱 中,
中,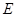 、
、 分别是
分别是 、
、 的中点,点
的中点,点 在
在 上,
上, .
.
求证:(1)EF∥平面ABC;
(2)平面
 平面
平面 .
.