(本题14分)如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米,建立适当的直角坐标系,(1)求抛物线方程.(2)若将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 
在如图所示的多面体中,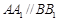 ,
, .
.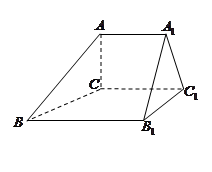
(Ⅰ)求证: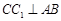 ;
;
(Ⅱ)求证: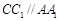 .
.
如图,在四棱锥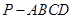 中,底面
中,底面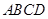 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且 交
交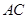 于点
于点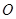 .
.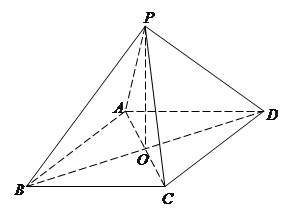
(Ⅰ)求证: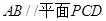 ;
;
(Ⅱ)求证: .
.
在平面直角坐标系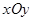 中,已知直线
中,已知直线 的斜率为
的斜率为 .
.
(Ⅰ)若直线 过点
过点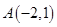 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若直线 在
在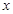 轴、
轴、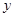 轴上的截距之和为
轴上的截距之和为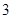 ,求直线
,求直线 的方程.
的方程.
已知a,b为常数,a¹0,函数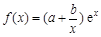 .
.
(1)若a=2,b=1,求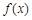 在(0,+∞)内的极值;
在(0,+∞)内的极值;
(2)①若a>0,b>0,求证: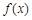 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若 ,
, ,且
,且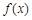 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点 形成的平面区域的面积.
形成的平面区域的面积.
设数列{an}满足an+1=2an+n2-4n+1.
(1)若a1=3,求证:存在 (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.