已知椭圆 :
:
 的左、右焦点分别为
的左、右焦点分别为 离心率
离心率
 ,点
,点 在且椭圆E上,
在且椭圆E上,
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求点
,求点 横坐标的取值范围.
横坐标的取值范围.
(Ⅲ)试用 表示
表示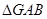 的面积,并求
的面积,并求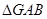 面积的最大值
面积的最大值
数列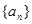 的前
的前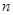 项和为
项和为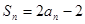 ,
,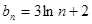 ,函数
,函数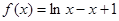 .
.
(1)求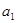 的值和数列
的值和数列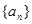 的通项公式;
的通项公式;
(2)证明:当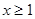 时,
时,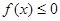 ;
;
(3)求证: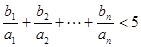 .
.
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点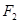 .点
.点 是曲线C1,C2在第一象限的交点,且
是曲线C1,C2在第一象限的交点,且 .
.
(1)求双曲线交点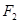 及另一交点
及另一交点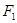 的坐标和点
的坐标和点 的坐标;
的坐标;
(2)求双曲线 的方程;
的方程;
(3)以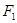 为圆心的圆M与直线
为圆心的圆M与直线 相切,圆N:
相切,圆N: ,过点P(1,
,过点P(1,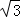 )作互相垂直且分别与圆M、圆N相交的直线
)作互相垂直且分别与圆M、圆N相交的直线 和
和 ,设
,设 被圆M截得的弦长为s,
被圆M截得的弦长为s, 被圆N截得的弦长为t,问:
被圆N截得的弦长为t,问: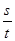 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.
在△ABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5,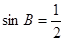 .
.
(1)求 和
和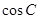 的值;
的值;
(2)设函数 ,求
,求 的值.
的值.
某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) |
1 |
2 |
3 |
4 |
| 药品产量:y(单位:万盒) |
3 |
4 |
5 |
6 |
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y= x+
x+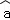 ;(参考数据
;(参考数据 i2=30,
i2=30, xiyi=50)
xiyi=50)
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?