已知向量 ,若
,若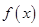 =
=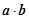
(Ⅰ)当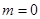 时,求
时,求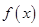 在区间
在区间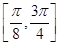 上的取值范围;
上的取值范围;
(Ⅱ)当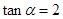 时,
时,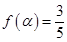 ,求
,求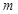 的值.
的值.
(本小题满分12分)如图,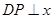 轴,点
轴,点 在
在 的延长线上,且
的延长线上,且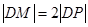 ,当点
,当点 在圆
在圆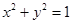 上运动时.
上运动时.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作圆
作圆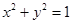 的切线
的切线 交曲线
交曲线 于
于 ,
, 两点,求
两点,求 面积
面积 的最大值和相应的点
的最大值和相应的点 的坐标.
的坐标.
(本小题满分12分)正方形 与梯形
与梯形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 在线段
在线段 上且不与
上且不与 重合.
重合.
(Ⅰ)当点 是
是 中点时,求证:
中点时,求证: ;
;
(Ⅱ)当平面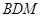 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥 的体积.
的体积.
(本小题满分12分)某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调 查结果如下表所示:
(Ⅰ)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(Ⅱ)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附: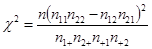 .
.
(本小题满分12分)设数列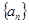 的各项均为正数,它的前
的各项均为正数,它的前 项和为
项和为 ,点
,点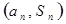 在函数
在函数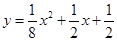 的图像上;数列
的图像上;数列 满足
满足 ,其中
,其中 .
.
(Ⅰ)求数列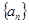 和
和 的通项公式;
的通项公式;
(Ⅱ)设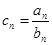 ,求证:数列
,求证:数列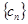 的前
的前 项和
项和 .
.
选修4-5:不等式证明选讲
已知 .
.
(1)解不等式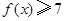 ;
;
(2)若关于 的不等式
的不等式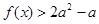 对任意的
对任意的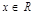 恒成立,求
恒成立,求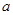 的取值范围.
的取值范围.