某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: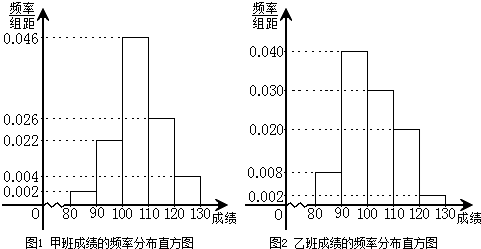
(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 |
成绩不小于100分 |
合计 |
|
| 甲班 |
a= _________ |
b= _________ |
50 |
| 乙班 |
c=24 |
d=26 |
50 |
| 合计 |
e= _________ |
f= _________ |
100 |
(Ⅱ)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ,其中n=a+b+c+d
,其中n=a+b+c+d
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
已知函数f(x)=x2+2alnx.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京召开.为了做好两会期间的接待服务工作,中国人民大学学生实践活动中心从7名学生会干部(其中男生4人,女生3人)中选3人参加两会的志愿者服务活动.
(Ⅰ)所选3人中女生人数为ξ,求ξ的分布列及数学期望:
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.
设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
对于任意正整数n,猜想2n﹣1与(n+1)2的大小关系,并给出证明.