(本题满分8分)
已知经过点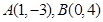 的圆
的圆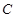 与圆
与圆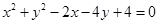 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线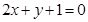 .
.
(Ⅰ)求圆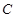 的方程;
的方程;
(Ⅱ)若动圆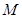 经过一定点
经过一定点 ,且与圆
,且与圆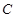 外切,求动圆圆心
外切,求动圆圆心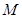 的轨迹方程.
的轨迹方程.
已知函数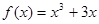
(1)求该函数的导函数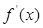 ;
;
(2)求曲线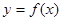 在点
在点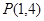 处的切线方程.
处的切线方程.
如图:已知三棱锥 中,
中, 面
面 ,
, ,
, ,
, 为
为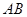 上一点,
上一点,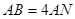 ,
, 分别为
分别为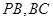 的中点.
的中点.
(1)证明: .
.
(2)求面 与面
与面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(3)在线段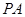 (包括端点)上是否存在一点
(包括端点)上是否存在一点 ,使
,使 平面
平面 ?若存在,确定
?若存在,确定 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.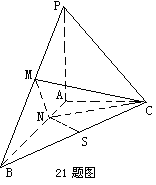
若抛物线的顶点是双曲线 的中心,焦点是双曲线的右顶点.
的中心,焦点是双曲线的右顶点.
(1)求抛物线的标准方程.
(2)若直线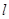 过点
过点 交抛物线于
交抛物线于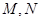 两点,是否存在直线
两点,是否存在直线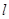 ,使得
,使得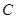 恰为弦
恰为弦 的中点?若存在,求出直线
的中点?若存在,求出直线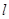 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
如右图,一个结晶体的形状为平行六面体,以点 为端点的三条棱
为端点的三条棱
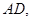
 的长都等于
的长都等于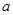 ,且彼此之间的夹角都是
,且彼此之间的夹角都是 .
.
(1)用向量
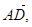
 表示向量
表示向量 .
.
(2)求晶体的对角线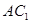 长.
长.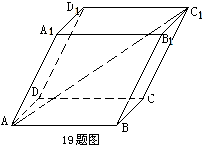
已知抛物线的顶点为椭圆
 的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点
的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.