已知:在矩形 中,
中, ,
, .分别以
.分别以 所在直线为
所在直线为 轴和
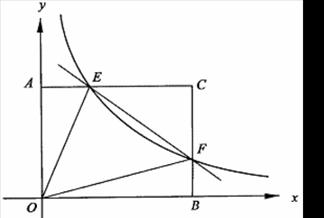
轴和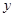 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系. 是边
是边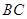 上的一个动点(不与
上的一个动点(不与 重合),过
重合),过 点的反比例函数
点的反比例函数 的图象与
的图象与 边交于点
边交于点 .
.
(1)求证:
 与
与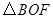 的面积相等;
的面积相等;(2)记
 ,求当
,求当 为何值时,
为何值时,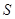 有最大值,最大值为多少
有最大值,最大值为多少 ?
?(3)请探索:是否存在这样的点
 ,使得将
,使得将 沿
沿 对折后,
对折后, 点恰好落在
点恰好落在 上?若存在,求出点
上?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(10分) 如图,Rt△ABC中,∠C = 90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上.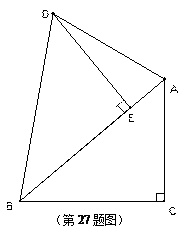
(1)若∠BDA = 70°,求∠BAC的度数.
(2)若BC = 8,AC = 6,求△ABD中AD边上的高.
(10分) 铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元?
(12分) 如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =" 10" cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
(10分) 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表(1)是该校学生阅读课外书籍情况统计表,图2是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人.请你根据图表中的信息,解答下列问题:
|
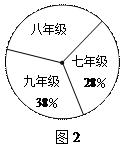
(10分) 如图,在方格纸(每个小正方形边长为1)中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1.
(1)请你在方格纸中画出梯形A1B1C1D1 ;
(2)以点C1为旋转中心,把 (1) 中画出的梯形绕点C1顺时针方向旋转 得到梯形A2B2C2D2,请你画出梯形A2B2C2D2.
得到梯形A2B2C2D2,请你画出梯形A2B2C2D2.